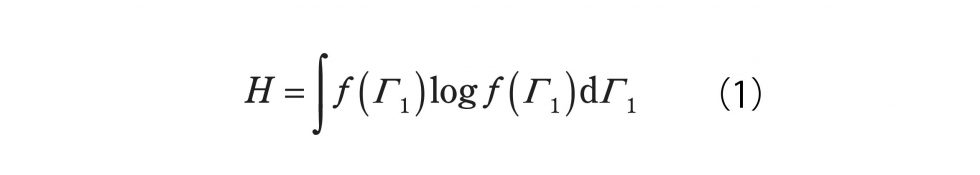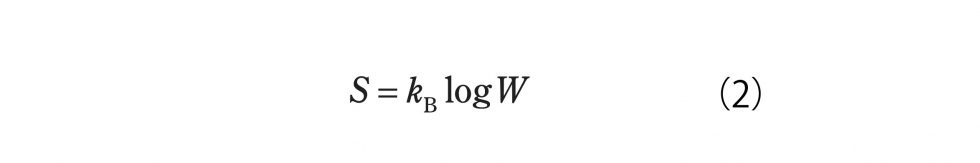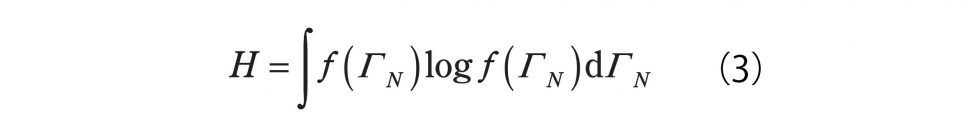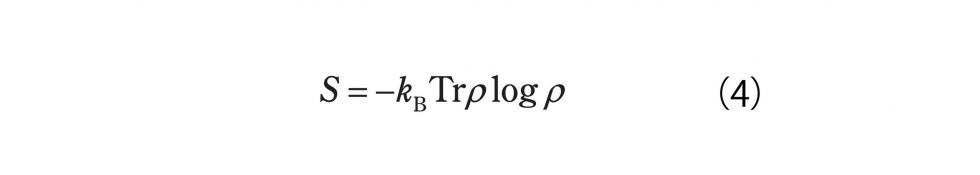「(理学の響宴) しゅんぽじおん」とは
プラトン(Platon)著の『饗宴』で書かれた、科学者が集まり、議論をしかけ、話を膨らませ、『知への愛、フィロソフィア』を説く饗宴。堅苦しくない場でざっくばらんに話し合うことで、新たなアイデアを生み出そうという試みです。

執筆:大阪大学 教授 橋本幸士
大阪大学素粒子論研究室
(大学院理学研究科 物理学専攻)
掲載元:パリティ
Vol.33 No.22 2018-02
2017年9月29日午後5時半、大阪大学理学部。教育研究交流棟の3階に、議論好きの科学者が、ぞろぞろと集まってきた。
理学の饗宴『しゅんぽじおん』である。その案内文には、こうある。
「研究科内外の研究者(教職員や大学院生のみなさん)、産業界の方々の研究交流を促すため、分野を超えた広い視野に立って新しい理学のタネを生み出すイベントです。ワインとチーズが振舞われる予定です。登録の必要はありませんので、金曜の夕刻、1時間程度、お気軽にお越しください」。
まあ、一言でいえば、お酒で交流しながら理学のあらゆる分野の講演を聴いて、新しい研究のタネを生み出そうや!というイベントである。
早くも第3回を迎えたが、第1回「時間とは?」、 第2回「カオスとは?」に引き続き、第3回、ついに「生命とは?」のお題。
自分の研究を詳細に話してもらうのではなく、自分の科学観に基づいて、いただいたお題について議論のネタを提供する、そんなことがスピーカーには要求されてしまうのである。
「生命」といえば、理学部のなかでも生物学専攻の教員が登壇するのが当然であろう。しかし、それではおもしろくない。そこで、今回の講演者は、化学専攻、そして宇宙地球科学専攻のそれぞれから、1人ずつお願いすることになった。
はたして、化学や宇宙の研究者が考える「生命」とは、いったい?!
会場には、若い大学院生の姿も多くみえる。細分化された理学のなかで、 壁を越えた先をみようという、
血気盛んな学生たち。頼もしい限りである。
化学者にとっての「生命」
登壇者:梶原康宏氏

化学者、梶原康宏さん
「梶原です。まあ今日はどうも録音もされてるし、冊子にもなると急にびびらされてしまって、10年くらい前に阪大に公募で来てですね、教授がウワーっと座ってその前でなんかしゃべって、ここでやっていけんのかな、って思ってたのを思い出してしまいました。もう皆さんお酒飲んでるからタチが悪くなるんではないかと今日は思っております」
(会場は爆笑)

「生命とは?僕、もともと有機化学なんで、できるだけ化学的な視点で眺めてみようかと思います。生命とは?って考えると、世のなかにはそれについて書いた有名な本があります。たとえば」
そういって梶原さんは、ある岩波文庫1)の表紙を、一部分を隠してみせた。
「それって、シュレーディンガーの本?」 との聴衆からの声が上がる。
「そう、物理の人がここにおると思って、みせました。まあ有名な本です。それと、福岡伸一先生の『生物と無生物の間』2)。出版時には一般にはこういう本がわかりやすかったでしょうね。つまり、生物は複製する、というのが定義である、ということです」
会場からは「まあ、そうやろな」といううなずきがみえる。
「化学からみた生命の話をしましょう。 2002年に制限酵素の発見でノーベル賞をとったスミス先生(Hamilton O. Smith)が、 2008年に、ケミカルに1DNAをつくって、生命体をつくろうという研究を始めたサイエンスの論文があります。バクテリアの58万2970個のDNA塩基対を人工的につくって、論文に出したんですね。うわ。すごいな、と。これ、化学ですよね」
「で、とうとう 2010年には、それでできた遺伝子をバクテリアの殻の中に入れたら、 DNAの複製が始まった3)。つまりCHEMISTRYで、生命体ができたっていうその最初のきっかけになったんですよ。だから、『化学で生命は語れるであろう』という発端になった論文なんですよね」
なるほど、化学者は、まず生命の根本である遺伝子を化学的に合成し操作することで、生命を理解しようとするのか。会場にはさまざまな分野の研究者が集まっていたが、自分の生命観との違いからか、もしくは化学による理解の進展への驚きからか、ざわざわとした雰囲気になった。
梶原さんはその雰囲気を察したのか、
「で、本当に理解できるか?っていうとまあ結論からいうとまあそんなに簡単ではないと、いうことです」
「遺伝子を化学で合成するだけではない、っちゅう話になるんですね?」と会場からの質問に、梶原さんは笑って 「そうです、そうです」と答えた。
「で、さっき冒頭でもお話ししたように、DNAで全部ヒトの設計図が描いてある、まあそれは間違いないんですけど、これ、そう単純じゃないわけですね。2004年にヒトのDNAが全部解読されて、まあ製薬会社もみんなこれが全部わかれば病気の原因も全部わかるからもうそれでバッチリだと思ったんですけど、そうは問屋がおろさなくて、この後いろいろDNAやできたタンパク質に飾りがついてさまざまな機能が発現していくということがわかったんですね。で、まあそういうことで、じつは生命は非常に複雑でDNAだけでは語れないということがわかってきた」
梶原さんは懐かしい写真をとり出してきた。

昔懐かしいOHP用のスライド「トラペ」
「これ、何かおわかりになりますでしょうか。むかーしの人はわかりますよね。 OHPの資料が自分の引き出しのなかで束になってたんでもってきました。昔はこれでプレゼンしてたんですね。パワーポイントがないからこうやっていたんですね。こう、束にしておくとゴチャゴチャでわかんなくなって、あー、どのスライドだったかな?と探したりした懐かしい思い出があるんじゃないかと思います。たしかに、重ねてみるとわからない。でも、 1枚パッと引き出してみるとじつは、シンプルな化学反応の図が描いてあるんですよ。 1枚1枚とってもシンプルで、じつは生命体というのは、こういった非常に単純な化学反応が複雑に積み重なっていって突如、生命体になっているに違いないというのがまあわれわれ、化学者の考え方ですね」
不肖僕も、学生のときには透明なOHPシートにマジックペンでセカセカと書いていたのを思い出した。ただし、こんなに汚くはまとめてへんかったけど (自負)。
しかし梶原さんの例は非常によくわかった。そしてその語りは続く。
「で、やはり生命体が複雑な理由を説明するのにわかりやすい例は、一卵性双生児なんですよね。たぶん、生まれて小ちゃい頃は、よく似てたんだと思うんだけど、だんだんこう、成長していくに従って、顔もお互い変わってくるんです。何が違うのかっていうとね、設計図は60兆個の細胞のなかにある DNA全部一緒で、何も変わらないはずなんですよ。でも、一番似てるはずの一卵性双生児のDNAにみられるように成長とともに何かが変わる。その発端を見いだしたのはガードン先生(J. B. Gurdon)で、 2012年に山中先生と一緒にノーベル賞とった人です。山中先生は、IPSで有名ですよね、で、その一方で、そのガードン先生のことは日本では、あんまり盛り上がりませんでしたよね。じつは、ガードン先生の実験が有名なんですよ」
会場から「おぉー」という声。

「この人が、ノーベル賞の発端をつくった。カエルの卵をとってきて細胞の核を抜き、オタマジャクシの皮膚からとった細胞の核を、入れたんです。つまり成熟して皮膚になっちゃってる細胞のDNAを受精していない卵子の核と入れ替えて、受精させたんです。そしたら、オタマジャクシができてカエルになった。という実験を最初にやった人なんです。これは、何を意味しているかというと、 DNAのリプログラミングが起こったっていう証明になったんです」
リプログラミング、これ、梶原さんの話のキーワードになりそうだ。
「リプログラミングとは何か?卵子と精子が受精するまでは、それぞれ半分の染色体をもっていて、それ全部にじつは、まあある修飾が施されている。大人になっていくための、皮膚になれ、あるいは骨になれ、心臓になれ、肝臓になれ、まあ、歯になれ、そういう修飾、目印が入っているんだけど、その目印が、受精するときには、パッと消えるんですね。それをリプログラミングというわけです」
「ガードンさんの実験で証明されたということですか?」
「そうです。なんでそれが大事かっていう話をしましょう」
梶原さんはスライド〈図1a〉をみせた。
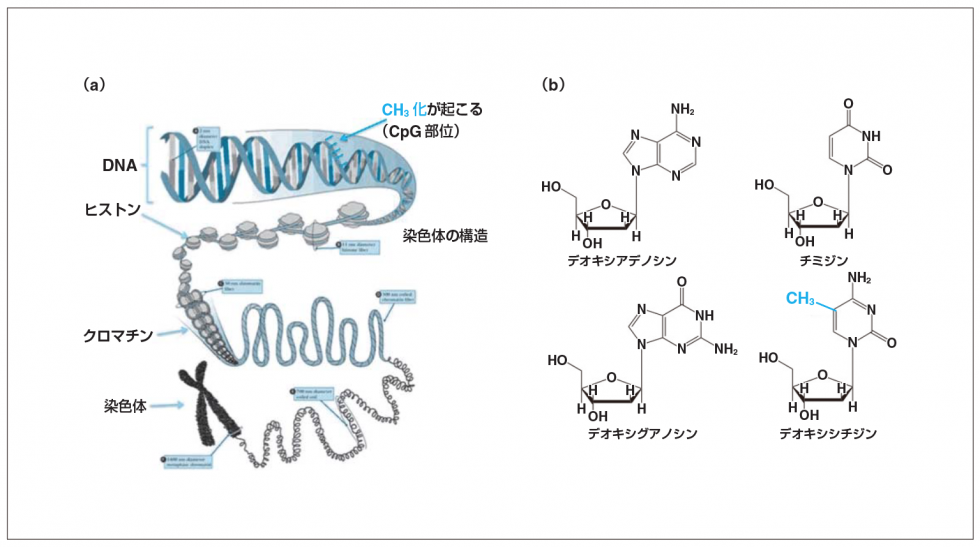
〈図1〉梶原さんのスライド
(a)DNAの構造、(b)DNAのメチル化。
「DNAの構造をみてみましょう。染色体を全部バーっとひもといていくと、クロマチンというタンパクにDNAが巻きつけられてる。それをさらに解いていくと、DNAの2重らせんがみえてくる。つまりわれわれの細胞のなかでは、DNAはこういうかたちでいるんですね。そこでだんだんメチル化されていく。メチル基ってじつは非常にシンプルな化学構造をしています。
DNAは4種類の化合物でつくられているんですね。デオキシアデノシンとか4つあってそれぞれA、 T、C、Gというふうに文字でいわれているわけです。問題となるのはそのメチル化は、塩基の5位の位置に起きます。この〈図1b〉の右下に書いたように炭素1個、水素3個、という非常に小さなものがつくだけで、一卵性双生児のような顔の変化が起こってくるということになるわけです。生命というのは、DNAだけで決まっているわけじゃない。そこにメチル化があって、コントロールされているんです」
僕は梶原さんの話においてけぼりを食ったので、正直に「ちょっとわかんなかったです」と質問してみた。
会場は笑いに包まれたが、聞くは一時の恥である。
「メチル化っていうのは、1人の人間でもDNAの違う場所に発生するんです?」
「そう、細胞によって、メチル化の場所が違うから、骨になったり皮膚になったり、いろんなものに分化するんですよ。こんな例で説明しましょうか。ロミオとジュリエットの話で“O Romeo, Romeo wherefore art thou Romeo?” (ロミオ、ロミオ、あなたはどうしてロミオなの?)という原作がありますよね。劇場で上演されるときには、このセリフが脚色されて、いろいろ変わってくるわけです。「ロミオ」を2回ではなく3回いったり、ね。それによって、劇のイメージが変わるわけですよ。一卵性双生児みたいにね。で、リプログラミングって、大もとの文章にもどるような感じですよね。この例で伝わりました?」

「なるほど、文章をDNAと考えると、わかりやすいですね。単語を落とした りすると意味が変わるわけやから」
「そう。それに、劇的な変化も起こってしまうことがあるんです。たとえばこの文章のなかの“art”のところに“f”がついて、 “fart”になったとしましょう。そしたら、『おなら』って意味になっちゃうんですよ(引用: N. Carey, The Epigenetics Revolution, Columbia Univ. Press;中山潤一訳『エピジェネティクス革命』丸善出版)」
見事な説明に、会場は爆笑。これで、リプログラミングの重要性が誰もの心にしみわたったようである。
そして、梶原さんは、いままで話したメチル化をはじめとする化学反応は、酵素というタンパク質がものすごい高速で働いて起こっているということを話した。 1秒間に10万回以上反応を起こすことができるそうだ。この酵素は、何やら遷移状態という反応が起こる瞬間の分子のかたちを維持することができるようだ。
「化学者には、この遷移状態の環境をガラス容器のなかで簡単につくれないので、生命システムに勝てないのだ」と梶原さん。
「DNAが生命体の道具である酵素をつくる指示を出し、そして3000種類ともいわれる酵素が、1つ1つ反応を間違えないように行い、それが複雑に絡み合って生命体になっているんです」
ふむ、生命の複雑さを一番よく理解しているのは、梶原さんのような化学者なのかもしれない。

宇宙物理学者の「生命」
登壇者:松尾太郎氏

宇宙物理学者、松尾さん
つぎに登場したのは、宇宙地球科学専攻の松尾太郎さん。
若手バリバリの宇宙生命の研究者は、「生命」をどんなふうに見ているんだろう。聴衆の僕らは、宇宙における生命探査がどんなに進んでいるかをこの後聞くことになるとは、まったく想像もしていなかった。

「10年前に私が学生の頃、『宇宙生命』とかいったらもう、頭がおかしい人みたいにみられましたね。でもいまは、もう、それが本当に天文学の中心になってます」
発展が著しい分野の先端のところを聞けるのは本当に嬉しいことである。
「で、まっ、簡単に自己紹介なんですけど、私は生命探査を本当にめざして10年間やってきてまして、とにかく独創的なアイデアを出さないと日本はたぶん勝てないというところであるので、そういう実験とか機械開発を中心にやってます!NASAが計画中の2020年に決まる宇宙望遠鏡のなかの1つのプロジェクトで生命の発見をめざしています。で、来年に NASAのエイムズ研究所に私のプロジェクトである宇宙生命探査装置が立ち上がります!なんで、いますごいワクワクしてると同時にですね、昨日寝てなくて、いまあの、やばい状態なんですが(笑)」
松尾さんの飛ばしっぷりに、聴衆の皆さんの目が輝く。
「いま、宇宙生命という探査の観点から、宇宙における生命とはどういうふうにみえてくるのかっていうのを、お話ししたいなと思っています。で、まず、宇宙生命を探す意義を3つ、みていきましょう。
第1に、われわれは天文学からスタートしてますが、天文学っていうのは考古学なんですね。 137億年っていう宇宙が始まってからの歴史をみるので、その歴史のなかで、生命を探すのは歴史の最後の出口の部分をみるっていうことです。
で、第2には、生命の誕生と多様性を探る方法としての意義です。これまではおもに、顕微鏡で生命の誕生をみているわけです。 昨日ちょうど、Natureの雑誌をみてたらですね、日本の先生がいままでグリーンランドで発見されていた38億年前の生命の痕跡よりさらに1.5億年前以上の生命が発見された、という論文4)が出てました」
松尾さんはスライドでそのNatureの論文の写真をみせた。
黒いつぶつぶのようなものが写真にみえる。皆、首をかしげて、「えぇぇ、これで生命が発見されたっていうんですか?」
松尾さんは笑いながら、
「えっとですね、13Cと12Cの2種類の炭素をみたときに、生物は基本的に12Cを好むので、それがより濃縮している岩が見つかると、その炭素、生物がいる兆候の1つの指針と考えられるわけです。それがカナダで発見されたということのようです」
「すいません、それは化石なんですか?この黒いつぶつぶのかたちが生命のかたちだと思ってもいいんですか?」
そんな聴衆からの厳しい質問に答えたのは、聴衆のなかの太陽系年代学にくわしい先生だった。
「あれ自身は炭化物。中の炭素の同位体の比率がちょっと違うってことなんですよね」
ほほぅ、という声が上がった。松尾さんの話は徐々にポイントに近づいてきた。
「で、こういう顕微鏡から天体望遠鏡に行こうとしているわけです。また別の角度からの生命探査ができるだろうと期待してます。そこで、第3の意義として、しかも最近一番とくに動きがあるのは、『宇宙で私たちは本当に1つなのか?あるいはもっと生命がありふれているのか?』ってことです。宇宙で私たちは孤独なのか?これが、私の研究の強い動機になっています」
そうか、宇宙の研究者は、生命を宇宙で実際に探してやろう、「生命とは」っていう科学はそこからやないか、という、まさに科学者の立場なんやな、僕はそう思った。
松尾さんは、宇宙生命を探す方法を紹介し始めた。
「宇宙生命を探したいと思ったとき、3つの方法がありますね。第1に、太陽系内で探す。第2に、知的生命(宇宙人)を探す。第3に、遠くの惑星で生命を探す。今日の私のテーマは、第3のものです。その前に、まず第1をみてみましょう。つまり、地球がいかに特異であるか?ってことですね。まず、宇宙生命を探そうと思ったら、近くから探しますね。火星から始まって。たとえば、土星にエンケラドスという衛星があって氷に覆われてるんですけども、エンケラドスの近くまでカッシーニ衛星が飛んでいって、太陽光がエンケラドスの表面あたりで吸収される様子が撮影されたんです。われわれ、これを水柱とよんでいて、氷の下に海があって、周期的に氷が割れたり閉じたりして海から水柱をつくっているんです。最近では、エウロパっていう土星の衛星も同じように、ハッブル宇宙望遠鏡で水柱を検出しています。われわれもそういうのをめざして最近、すばる望遠鏡でとらえようとしています」

「で、第2の点をみてみましょう。宇宙人はいるのか?みなさん、SETI(search for extra-terrestrial intelligence)って聞いたことあるでしょう。ETを探すプロジェクトです。一番わかりやすい例ですが、特殊な電波を地球から発信して、特殊な電波を返してくれるはずだから、そういう電波を探そう、というものです。実際『ワオ!シグナル』っていう、それっぽい電波信号を受信したことがあるんですけど、ただそれが本当に知的生命なのかどうかっていうのは、まだわかっていません」
宇宙人の話になり、会場は一気に盛り上がり始めた。
「たしかスクリーンセーバーみたいにパソコンにインストールして全世界でやったよね」
「見つかったんやっけ?」
「どないしたら見つかったって決まるんやろ」
「ラジオみたいなん聞こえたらオッケーとか?」
松尾さんがそこに割って入り、
「特異なシグナルは観測されてます。ただし、それがわれわれの知らないような未知の天体からかもしれない。γ 線バーストとよばれるような高エネルギー天体がこういうことを起こす可能性はあって、そことの区別がつかないというのもあります」
「オバマは予算を継続したけど、トランプはどうしました?(笑)」
「それは、わかんないです(笑)。あ、でも、中国が結構そういう予算をかけていますね。ただ私の話はそっち方向じゃなくて(笑)、第3の方針、遠くの惑星で生命を探す、ってものです」
松尾さんは宇宙人談義を打ち切り、次のスライドを見せた。〈図2〉
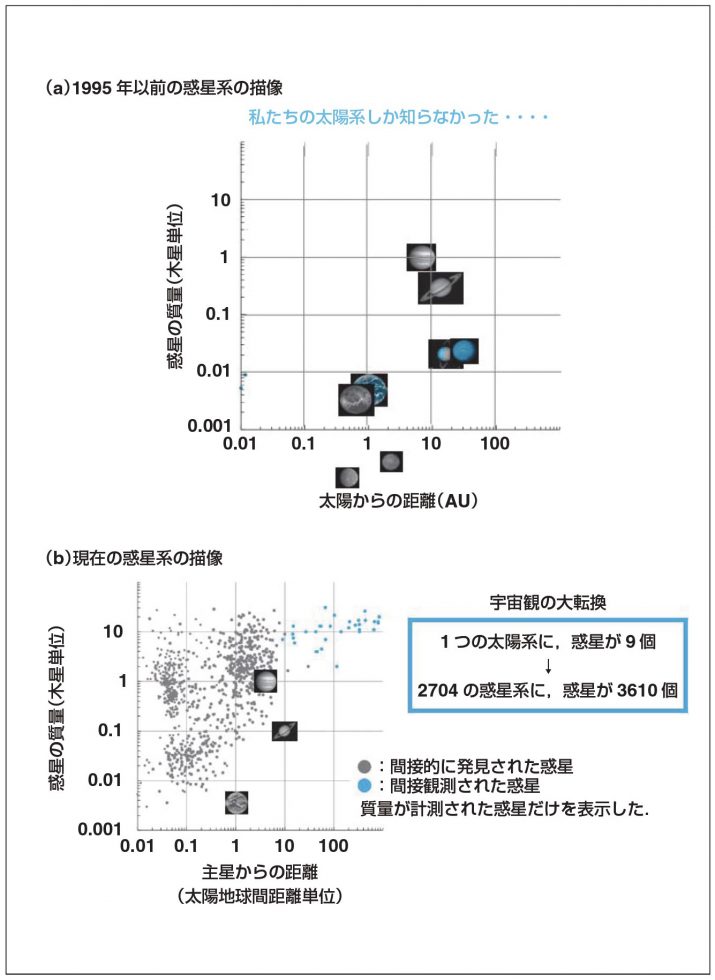
〈図2〉松尾さんのスライド「惑星系の描像の変化」
「1995年以前は、私たちの太陽系しか知らなかったんですよね。太陽からの距離と質量のグラフです。これが、この20年で、いま、2700の惑星系で、惑星が3600個も見つかっているわけです。つまり、大変期待がもてる状況になっているんです。それに、ケプラー衛星というのが、惑星のサイズを正確に測ることができる。その統計によると、太陽近傍の恒星のうちの3割は、地球サイズの惑星をもっていることが判明したんです」
系外惑星の観測結果はそこまで進んでいるのか、と驚かざるを得なかった。
「2017年には、太陽から30光年先の恒星系で、7個の地球サイズの惑星が公転していて、3個は液体の水をもつ可能性があるというものが発見されました。これをトラピスト1(Trappist-1)とよんでいます〈図3〉。つまり、ようやく今年(2017年)、地球の近傍で生命を宿す可能性のある惑星が発見されました。ただし惑星の物理量、つまり半径や質量、主星からの距離、のみが推定されています。そういう惑星に対して、今後観測を詳細に行うことで生命が存在するかどうかを探っていく、そういう重要な時期にさしかかっています。
では、皆さんに問いかけをしたいのですが、宇宙のなかで、ほかの惑星上に生命を探すなら、何を探したらいいでしょうか?」
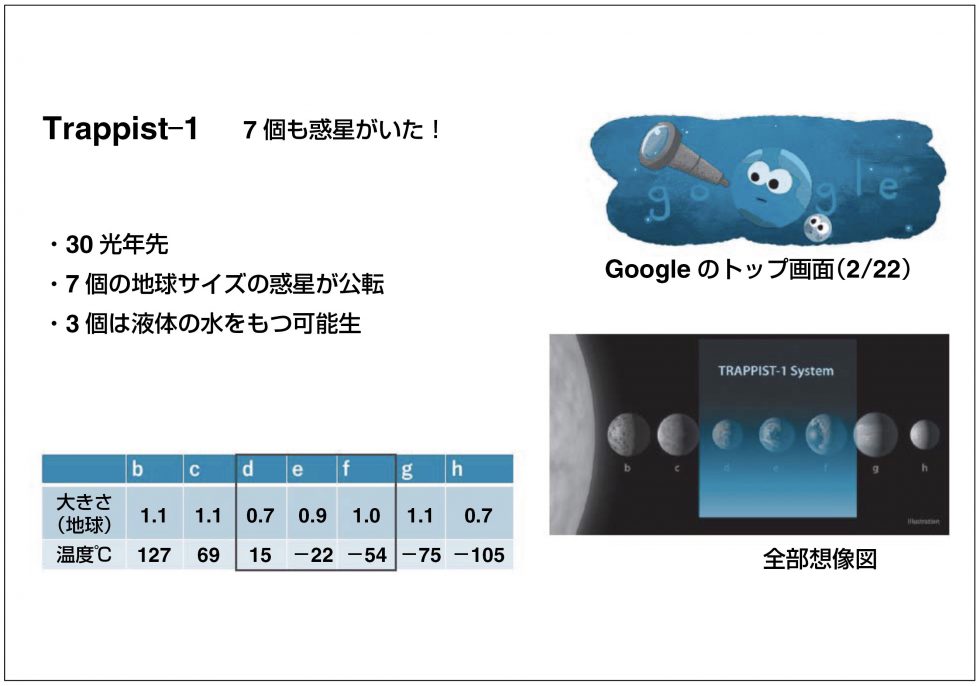
〈図3〉松尾さんのスライド「トラピスト1の惑星系」
僕の頭のなかは宇宙人モードで止まっていたので、いったんそれを白紙にもどし、考え始めた。まわりの聴衆も、「隕石かな」「もっと遠くの観測かな」などと相談している。松尾さんは、総括した。
「宇宙のなかで、地球が特異な点は何でしょうか? 私は、生物由来の酸素であるオゾンの存在、そして酸化と還元物質の非平衡状態にある大気、これらのスペクトル観測が決定的なのではと考え、NASAの大型計画でトランジット惑星のための分光装置を立案しているんです」
現在、太陽系外惑星の生命探査として、2020年に決まる4つの大型計画候補があるとのことだ。その望遠鏡が実際に動きだし、観測が開始されたとき、僕たちは宇宙に生命のたしかな痕跡を見つけだせるんだろうか。
松尾さんの講演の後も、松尾さんと梶原さんをとり囲んで、質問と議論が続いた。

ワインの時間にもかかわらず厳しい質問をされ、頭をかく松尾さん
「生命とは?」というテーマは、これまでもさまざまな科学者が挑んできたテーマに違いない。理学の饗宴『しゅんぽじおん』に参加する研究者や大学院生は、自分なりの科学観をもって来ているようだ。新しい科学の成果や、他分野の考え方を知り、自分の科学観を試すよい機会になっている。次回も、専門が楽しくぶつかり合う様子が堪能される会になるに違いない。
『しゅんぽじおん』は、徐々に解散するしくみである。
ワインも尽きた会場に最後までしぶとく残っていた6人は、梶原さんの
「あ?あ!このアイデア、いけるかもしれない!いけるかも!!」
という叫びを聞いた。
あの叫びがどうなったのか、次回の会場で梶原さんに聞いてみよう。
参考文献
1) シュレーディンガー:『生命とは何か―物理的にみた生細胞』(岩波書店、2008)
2) 福岡伸一:『生物と無生物のあいだ』(講談社、,2007)
3) H. O. Smith et al.: Creation of a Bacterial Cell Controlled by a Chemically Synthesized Genome, Science 329, 52(2010).
4) T. Tashiro et al.: Early trace of life from 3.95 Gasedimentary rocks in Labrador, Canada Nature 549, 516(2017).