「(理学の響宴) しゅんぽじおん」とは
プラトン(Platon)著の『饗宴』で書かれた、科学者が集まり、議論をしかけ、話を膨らませ、『知への愛、フィロソフィア』を説く饗宴。堅苦しくない場でざっくばらんに話し合うことで、新たなアイデアを生み出そうという試みです。

執筆:大阪大学 教授 橋本幸士
大阪大学素粒子論研究室
(大学院理学研究科 物理学専攻)
掲載元:パリティ
Vol.33 No.05 2018-05
2017年11月8日午後5時半、大阪大学理学部。ついに理学の饗宴『しゅんぽじおん』で、その主題を「エントロピー」とするときがやってきた。
そもそも、ワインとチーズを楽しみながら、理学のキーワードを肴(さかな)にして、わいわい議論しようや、という会なのであるが、そこに「エントロピー」とかいう小難しいキーワードが現れて、はたしてワインを楽しむ余裕が出てくるのだろうか。
そんな不穏な雰囲気を感じながら、続々と研究者や大学院生が集まり始めた。
『しゅんぽじおん』も第4回を迎えたが、第1回「時間とは?」、第2回「カオスとは?」、第3回「生命とは?」と続いたお題に比べると、「エントロピーとは?」はかなり敷居が高い気もする。
「う~ん、今回のお題はエントロピーですからねぇ」
と、私は隣りにいつも座っている基礎理学研究センターのセンター長の豊田さんに話しかけた。
豊田さんは、「どうなるんでしょうねぇ、とりあえずワイン飲みましょうか」と、のんきな答えである。
そのときわれわれはまだ、今回の講演が「エントロピーって難しい」派と「エントロピーって簡単」派の対決になろうとは、まったく想像もしていなかった。
今回の講演者は、物理学者の湯川諭さんと、化学者の中野元裕さんである。おふたりがミーティングスペースに現れたので、「今日の順番、どちらが先にします?」と尋ねてみた。そう、そんなことすらあらかじめ決まっていない、ざっくばらんな会なのである。
いろいろと相談したところ、ワインの酔いが回る前に物理学者の湯川さんの数式をみておいたほうがよいのでは、という至極真っ当な意見が出て、湯川さんが先に話すことになった(あとで思い出してみても、この選択はまったく正しかったのである)。
物理学者の「エントロピー」

登壇者:湯川諭氏
物理学者、湯川諭さん
「エントロピーって、難しいですよね、いろんな定義があって」
「こんにちは、初めまして。宇宙地球科学専攻の湯川といいます。橋本さんからメールをいただきまして、今日はこんな機会をいただきましてどうもありがとうございます。すでにもういっぱい飲んでしまって、何杯かわかりませんけども。いくらでもいただきます」
湯川さんも、ちゃんとワインを飲んでいるらしい。素晴らしいスピーカーである。皆、質問しやすくなるだろう。
「あの、じつは僕、この会に今日は初めて来させていただきまして、どんな感じか全然わからなくて、タイトルも何もなしで出てきてます(笑)。統計物理学を専門にしてまして、まぁふだんは非平衡の基礎のほうから、パターンとか交通渋滞とか、古典的な基礎的なとこからゲテモノのほうまで『非平衡』というキーワードでいろいろやってます。今日は『エントロピー』というお題で、ということなんで、最近のわれわれの業界で発展してきたこととかを含めて、まとめて10枚くらいスライドをもってきたんですけど、えっと時間は何分でしたっけ?」
聴衆から「プラスマイナス15分」という声が飛ぶ。
そこに聴衆から「マイナスもあるんか」のツッコミあり(一同爆笑)。
「僕、統計物理学者なんですけど、エントロピーって何かやっぱりよくわからない。ですね。わりと皆さんそういう感じの印象あるかもしれませんけど、やっぱりあの統計物理学を研究してるっていってもやっぱりわかんなくって。まあよく考えるとわかんないから統計物理学を研究してるのかなっていう気もしないではなくって、高校のときとか確率とか全然わからなくて、わかんないから統計物理を始めたというような気もするんです(笑)」
湯川さんにそういわれると、エントロピーが感覚的にわからなくても、ちょっと救われる気がする。
「いずれにせよ、どういう面でわからないのかなあということをつらつら考えてみると、たぶんですね、定義がいっぱいある、ということが問題なんですね。『エントロピー』って一言でみんないうんだけれど、定義がいっぱいあって。1番スタンダードなやつが、学部の1年生2年生ぐらいで習う『熱力学エントロピー』ってやつで、平衡状態に外からなんか仕事を加えたり、準静的に変化させたりしながら、平衡状態を移動させるということをやります。そのあいだに、準静的にゆっくりやりながら平衡状態を保つということをやりながら熱の出入りを勘定してやって、温度で割ったやつを積分したら、それが基準状態に対するエントロピーという量を与える、という定義です。これはクラウジウス(Clausius)が最初にいい出した、たぶん1865年くらいの定義ですね」
湯川さんは冒頭のスライド〈図1〉を指さしながら定義を説明した。次のページには、さまざまな定義らしき式が並んでいる。

〈図1〉 湯川さんのスライド「熱力学的エントロピー」「統計力学的エントロピー」
「ところが、そのうち3年生になると統計力学を習います。そんとき、じゃあ熱力学で習ったエントロピーってどう定義しますかっていうと、全然似ても似つかない定義が山ほど出てくるんですね。たとえばこの最初の式。
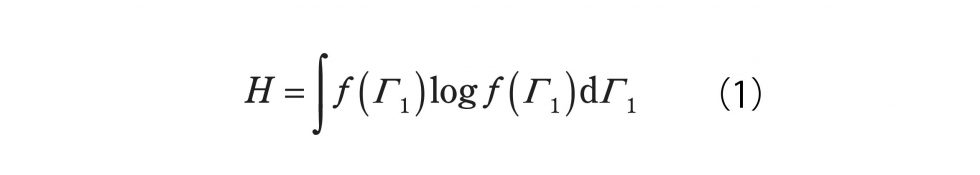
この式を出したのはボルツマン(Boltzman)が多分最初くらいだと思うんですが、文献とか人によってはこの式はエントロピーじゃないといっている人もいます。何でかっていうと、これは一体問題の式だから、という意見です。f(Γ1)というのは1粒子の気体分子のエネルギーの分布関数です。ボルツマンはそもそもボルツマン方程式という一体問題の運動を詳細に運動論で研究して、その過程で、あの熱力学第2法則のようなことを考えるためにこのH関数を定義しました。Hというのはf log f の期待値ですが、これが単調減少するといいました。でもボルツマンの最初の式って、この一体問題の式だから、物理系として1つの系をみたときに、多体でそれが本当に全体の正しいエントロピーかどうか、っていうのはよくわからないですね。その後で、ボルツマンは正しい
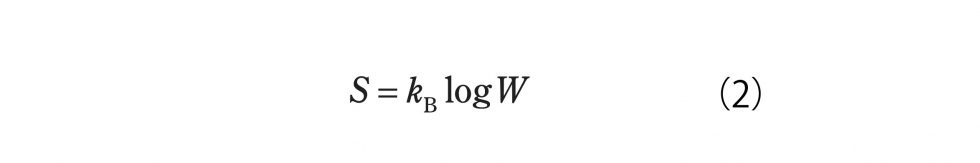
という有名な式を出してます。僕の共同研究者からもらったボルツマンのお墓の写真をみると、お墓にはこの有名な式が刻まれています」
お墓の写真に見とれる聴衆。
「Wというのは状態の数ですね。ミクロな立場の統計力学での、Wという勘定できる状態の数から、熱力学でいうエントロピーと対応関係があるんだ、というのを最初に出したのがボルツマンです」
みな、熱力学的なエントロピーと、統計力学的なエントロピーの式が等しい、という学部の頃に習ったことを思い出し、うなずいている。
「ギブス(Gibbs)も似たようなことをいってるんですが、多体系になっています。ボルツマンのもともとの話は、いわゆるミクロカノニカルアンサンブル、つまり、全エネルギーと体積と粒子数が保存しているときにWが勘定できて、それからSが定義できるっていうのをやったんですが、ギブスはもうちょっと一般的に、考えてる系の全体の分布関数を用いました。
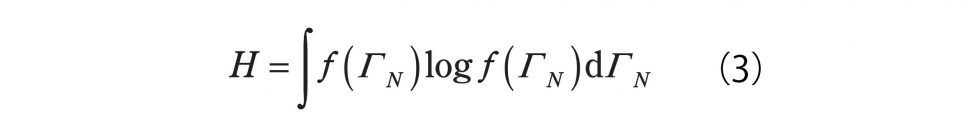
つまり積分のこの引数はアボガドロ数個あって、これはエントロピーだと最初にいったのはギブスです。で、これはアンサンブルとは関係なくいつでも統計力学的に正しいので、ギブスがまあ一番最初に導入したということになります。1902年と書きましたが、これはギブスの教科書の出版年代で、一方ギブスがどの論文でいってるのか探したんですがわかりませんでした。このなかでもしご存知の人がいたら教えてください」
そこで聴衆から質問が入った。
「教科書で新しいことをいったっていう可能性もあるんですか?」
「あるかもしれないんですが、ちょっとそこは私にはわからなくって。ギブス論文選集とか洋書の古書とかもってるんですけど、そこにはこんな話は全然書いてなくて。1902年のは、有名な教科書ですね。いま、プロジェクト・グーテンベルクでpublic domainになってるんで、丸ごとダウンロードできます1)。TeXで製版し直されていて、すごく読みやすくなっています」
それを聞いて、メモする人もちらほら。
「その後にフォン・ノイマン(von Neumann)が、量子力学で
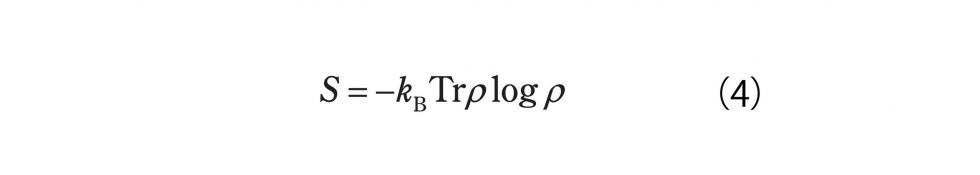
っていう話を出しています。これは最近の統計力学物理の発展では関係があるんですが、フォン・ノイマンの1929年の論文ってたぶんドイツ語で書かれてるんですけど、ずーっと忘れられてたんです。ノイマンは量子系が純粋状態でも熱平衡に緩和する、ということを議論してて、それがずーっと忘れられていました。2010年に発掘されて英訳されたのが、プレプリントサーバに上がって、知られるようになりました2)。
最近の統計力学のトピックの1つで『純粋状態でどうやって熱平衡に緩和するか?』という問題があります。波動関数を1個だけもってきたときに、それが時間発展して熱平衡状態になって、ということを議論するんですが、じつはフォン・ノイマンが見つけてやってた、っていう感じ。このとき、フォン・ノイマンは対応するエントロピーを2つぐらい出していまして、問題ごとにどのエントロピーを考えるべきかという論文が3つくらい出ているんです。そういうところにもじつはエントロピーの定義の多様性というのがみえてしまっていますね」
ふぅむ、エントロピーって一言でいっても、いろんな定義や見方があるんやな、そりゃなかなか感覚的にはとっつきにくいはずやわ、という感想が心をよぎる。
しかし、湯川さんはそこに畳み掛けて、
「ところがまだエントロピーっていうのはありましてね」と笑いながら、「公理論的エントロピー」の説明を始めた。
たまらず、「それってどんなことで役に立つんですか?」という禁断の問いを僕は発してしまった。
湯川さんはニコリと笑顔で
「それがねぇ、いろいろと使われているようなんですよ」と答える。
その後、議論は熱力学第2法則、シャノン(Shannon)の情報論的エントロピー、そして情報熱力学へとつながった。適切に物理系の情報量を知るには、適切なエントロピーの定義と使用法が必要なようである。
そこで「ゆらぎの定理」が言及されるに及んで、僕は、隣りに座っている豊田さんにこっそり話した。
「次の『しゅんぽじおん』のテーマは『ゆらぎ』ですな」
湯川さんの1時間に及ぶ議論が、ワインを注ぎながら行われて、「エントロピーって結局何だろう?」の言葉が会場のあちこちで聞こえる。
そこに立ち上がったのが、今日2人目の講演者、化学者の中野元裕さんであった。
化学者の「エントロピー」

登壇者:中野元裕氏
化学者、中野元裕さん
「エントロピーって、簡単ですよ。測れるんですもん」
「こんにちは、構造熱科学研究センターからやってきました中野と申します。構造熱科学研究センターというのは、じつは38年前に創立された研究室でして、一番最初、僕が学生で配属された頃には化学熱学実験施設っていう名前でした。そのファウンダーが関集三先生で、湯川先生は最新の話題をされてましたけれども、僕はこの創立者の関先生の時代にわかった昔話をさせていただこうかと思います(笑)」
中野さんのひょうひょうとしたしゃべりに引き込まれそうになった。エントロピーの長い歴史は、化学の測定の昔話でわかってしまうのか、と皆、耳をそばだてる。
「まず、熱容量っていうのは、化学のほうでのいい方で、物理の人たちはたいがい『比熱』っていいます。化学の人たちが比熱っていいたがらないのは、なんでかっていうと、比熱は熱じゃないじゃんっていう理由でして(笑)」
たしかに、比熱は熱の種類とはちゃうやんなぁ、と会場の人たちもうなずいている。
「熱って何かっていうと、ある場所にあったエネルギーが別の場所へ移動したときに、移動した差分のことですよね。熱容量っていうのは、ある物質がもともともってる物性値で、熱の移動とかなんとか関係なしにもともとあるものなんです。で、熱じゃないのに、比熱っていうのは気持ち悪いな、っていうことで化学の人たちは『熱容量』っていういい方を使います」
こんなところにも、分野の常識の違いが現れるんやね。
「で、実際に熱容量を測っちゃうと、エントロピーを実測できるんです!エントロピーは実験的に決定できる、ということです。今日は、湯川先生が式がいっぱいの解説をされましたが、僕の話はそれが測定ですぐみえるという話で……」
一同爆笑してしまった。湯川さんのさまざまなエントロピーの定義は、何だったんだろう?頭のなかがモヤモヤしつつも、中野さんの話にみるみる引き込まれてしまう。
「『エントロピー』ってこんなんか、っていうのが感覚的にわかってもらえればいいかなって思ってます。実生活上でのエントロピーをみてもらおうと思います」
会場から「おおっ」という声が上がる。「実生活上のエントロピー」って、魅力的な言葉や……。
「では、エントロピーの測り方を説明します。これは僕が4年生のときに使っていた熱量計です〈図2〉。断熱型という種類の熱量計で、原理は簡単です。熱の出入りがない状態でヒーターであるエネルギーを与えてやったときに、何度温度が上がったのかがわかれば、熱容量を計算することができる。そういうものすごい単純な理屈からできてます」
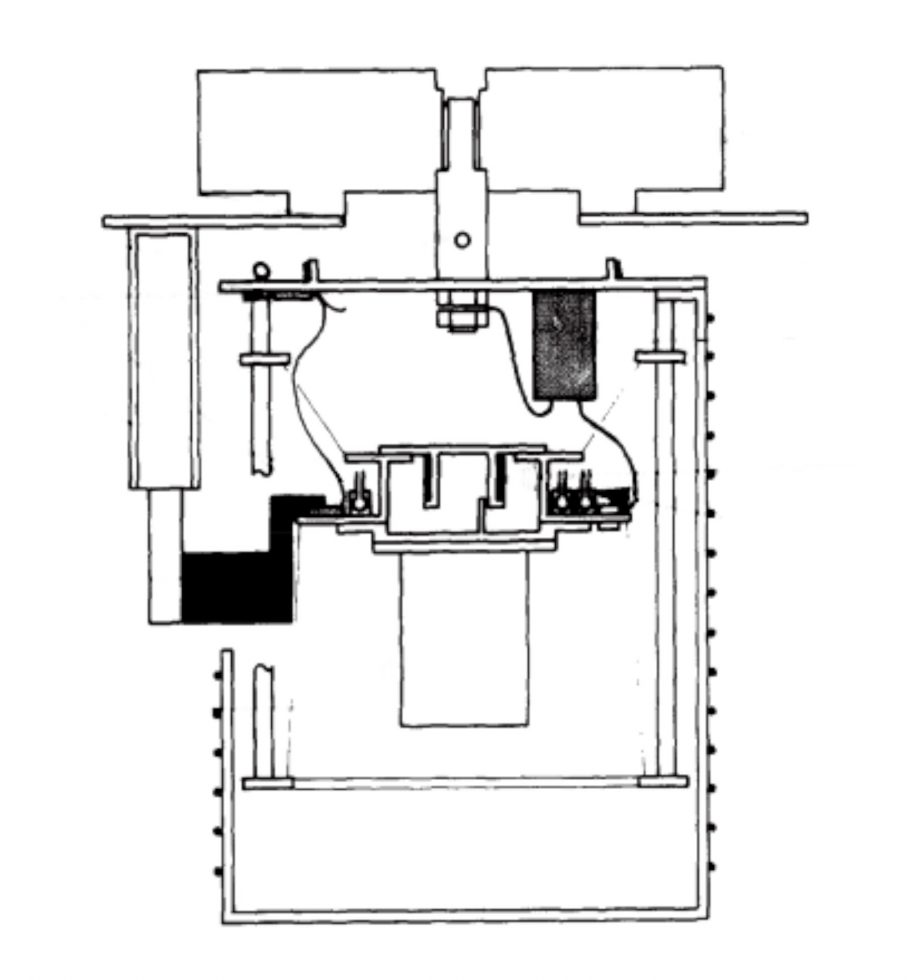
〈図2〉熱量計の構造図
「ここにぶら下がってますバケツのなかに熱容量を測りたいものを入れてやります。このバケツは、ヒーターと温度計のユニットにくっついているんですけど、そのユニットごと中空にナイロンテグスでぶら下げられてます。で、ここのヒーターでエネルギーを加えて温度計で温度の変化を読みとるわけです。そのときに熱の出入りがないようにするにはどうすればいいかということですが、熱が伝達するメカニズムとしては対流と伝導と放射があります。対流を遮断するには、まわりを真空に引いておけばいい。伝導っていうのは、十分に注意してリード線なんかを温度コントロールして温度差ができないようにしてやれば、ほぼ除くことができる。
あと、厄介なのは輻射なんですけれど、まわりに容器をつくって、容器の壁をバケツの壁と同じ温度にしてやれば、実質的に放射ではエネルギーを失わないということで遮断できます。外側の壁にヒーター巻いて、温度コントロールで『断熱制御』するんです。そうすると、電流で加えたジュール熱Qと温度変化ΔTが読みとれますから、 熱容量Cpは加えたエネルギーを温度差で割り算したもの、
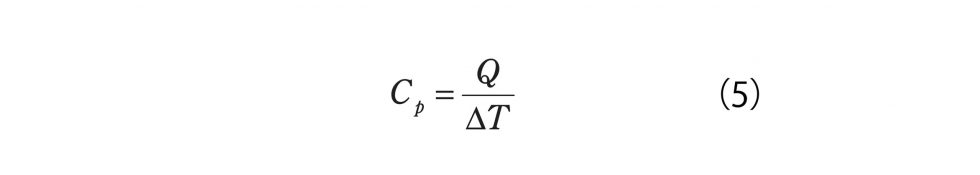
というかたちで簡単に測れちゃうんです」
一同、静まり返った。反論なし(笑)。
「で、熱容量をずうーっと温度を変えながら測って、logTという横軸で、積分してやったのがエントロピーです。
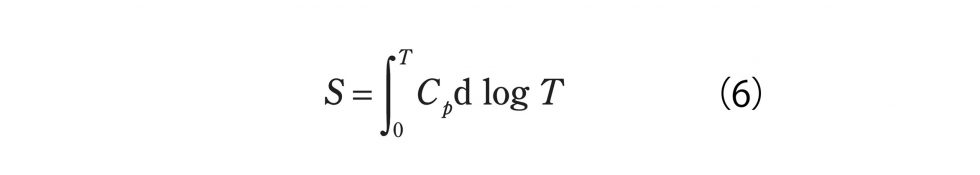
ですから熱容量を1点1点下からずーっと計っていくと、簡単にエントロピーって測定できちゃうわけですよ。で、えっとこういう測定法で、『エントロピーってこれや』っていうたら終わりじゃないですか(笑)」
終わってしまった。みな顔を見合わせながら、ニヤニヤしている。
「昔から僕、本当にこれで計れてるのかなあ、これでいいのかなぁって思ってたんですけど、ちゃんと計れちゃうんですよねー。それをお見せしましょう」
中野さんはスライド〈図3〉を見せた。
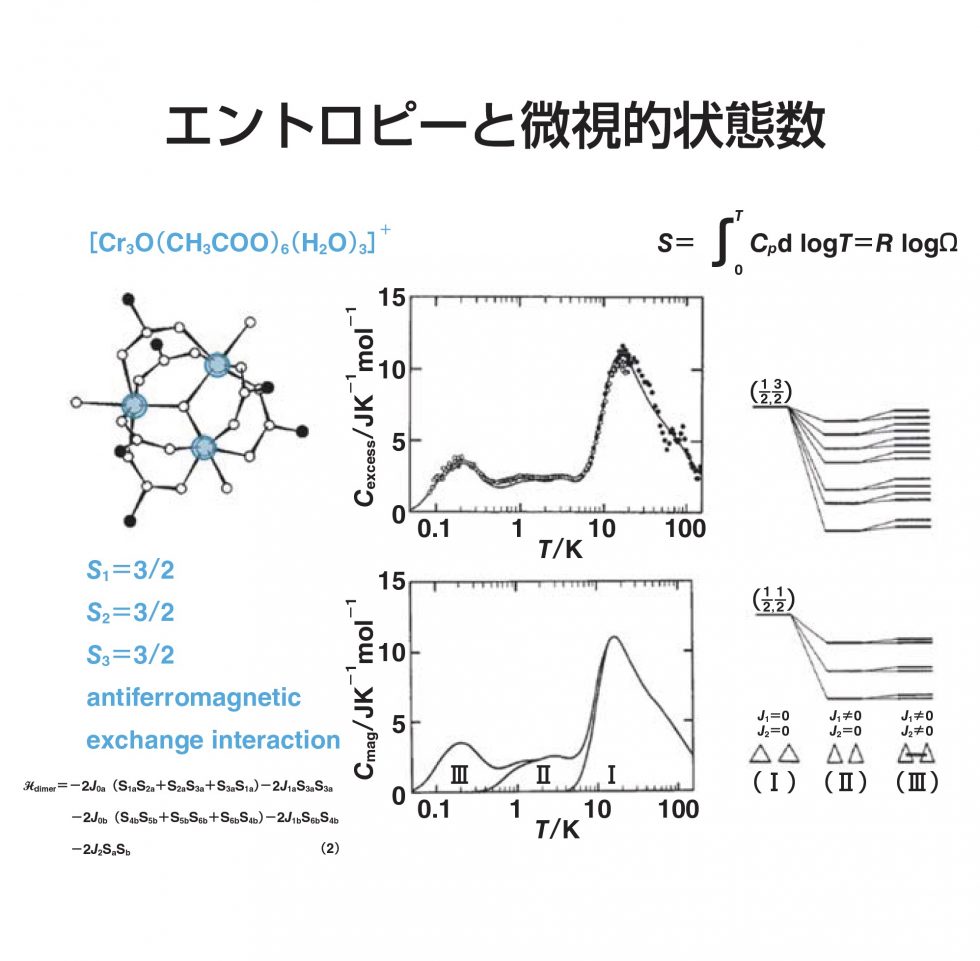
〈図3〉 中野さんのスライド「エントロピーと微視的状態数」
文献3より。antiferromagnetic exchange interactionは、反強磁性交換相互作用。
「われわれの学生だった時代には大量のサンプルが必要で、このバケツの容積が14cm3、サンプルが10gとか欲しかったんですね。だけど、いまは単結晶1個ね。ミリグラム、マイクログラム、っていうサンプルがあれば熱容量が計れる時代になってきました。非常にいい時代です。で、これは僕が4年生のときに計った熱容量です。僕は化学の人なのでちょっと化学っぽい物質を使いましたけれども、『クロムの3核錯体』といって、クロム金属イオンが1つの分子のなかに3個ほぼ正三角形に近いようなかたちで入ってる分子です。
クロムのイオンの上には電子が3個あって、スピン3/2をもってます。真ん中の酸素イオンで架け橋されてると、スピンのベクトルがどっちを向いたほうが居心地がいいっていうのが、変化します。交換相互作用っていいます。その結果、スピンのエネルギー準位がばらけてくるという現象が起こります。スピン準位がどんなふうにばらけてくるかということを、スライドの右に模式的に書いてます。まず(I)、スピンとスピンのあいだの相互作用が正三角形のとき、対称性が高いから、あんまりばらけません。それがね、(II)でちょっとゆがんで二等辺三角形になるとバラバラってもっと割れてきます。今度は(III)、2つの分子に相互作用が起こってしまいますと、割れます。これを、先ほど湯川さんにお見せいただいた統計力学の式にポッと入れてやったら、熱容量が計算できます。このグラフの実線が、計算結果ですね。んで、グラフのなかでポチポチポチって打ってあるのが、実測データです。みていただくとわかると思いますけど、正三角形になるよって割れた部分、それから二等辺三角形になって割れた部分、それから、最後の2つの分子間の相互作用で割れちゃった部分というのが全部、きれいにみえてきて、こんなかたちで熱容量がパーンと合っちゃいます。横軸は温度のlogなので、このグラフの上の面積がそのままエントロピーになってるんです。湯川さんの話のなかの、一番わかりやすいエントロピーですね、出ちゃいました」
会場は爆笑に包まれた。
「で、(III)のところの面積を積分で求めてやると、R log 2 っていう値が出てきます。これは何でしょうか。じつは、エネルギー準位が2つに分裂してる。熱エネルギーが大きくなってきたときに、そのエネルギー準位が区別がつかなくなって、縮重しているってみえているときに、そのときもっているエントロピーがR log 2だよ、微視的状態数が2になったんだよということがそのまま実測のエントロピーとしてみえているわけです。(II)のところまでを同じように積分するとR log 12に一致します。最後の(I)まで積分すれば、スピン3/2の4準位が3つあるってことで43で64準位ありますから、R log 64になって、実験と一致します。なんかね、理論と合っちゃう!」
会場の盛り上がりが最高潮に達したとき、聴衆のなかに座っていた湯川さんが口を挟んだ。
「じゃあ、T=0でのエントロピーがゼロだという、原点を決める問題は、実験ではどう決めるんですか」
中野さんは優しい声で厳しく答える。
「気体の状態のエントロピーは、ザッカー-テトローデ(Sackur-Tetrode)の式というのがあって、わかってるんですね。それで、気体の状態から温度が一番下に下がるまで、ぜーんぶ熱容量を測ります。実験で上から温度を下げていくときに潜熱とか全部測って、わかっているエントロピーの値から引いていってやると、温度ゼロではエントロピーがゼロ、って測れることになるんですね」
おお、わかるんや……。
その後、ガラスの転移でエントロピーが測れる話など、中野さんはいろいろなおもしろい実験例を教えてくれた。
でも聴衆はまず、エントロピーが美しく実験で測定できているという事実を大変楽しんだようで、その後の例の詳細は、ワインを飲んだ僕には記憶が薄れてしまった。『しゅんぽじおん』ではいつものことである。ワインとチーズが入っているのだから。
ただ「エントロピー」という深遠そうな話題も、理学の饗宴の舞台に乗ってしまえば、こんなふうに「美味しく」料理されてしまうのか、ということについては、参加者一同の共通の感想なのでは、と思う。次回はもっと難しい言葉をテーマにしてみるのもよいかも?
「エンタルピーでいこか?!」の声は、無視されたらしい。
参考文献
1) J. W. Gibbs: Elementary Principles in Statistical Mechanics (Charles Scribner’s Son’s, 1902);
プロジェクト・グーテンベルクのページはこちら:http://www.gutenberg.org/ebooks/50992.
2) J. von Neumann: Z. Phys. 57, 30(1929); R.Tumulka(trans.): Eur. Phys. J. H 35, 201(2010); arXiv:1003.2133(2010).
3) M. Nakano et al.: J. Phys. Chem. Solids 49,987(1988)